Geometries are a common cause of friction in geospatial data processing, especially when working with shapes that cross the antimeridian or cover a pole. Tilebox minimizes this friction, but adhering to the following best practices ensures optimal results. In doing so, you can ensure that no geometry related issues will arise even when interfacing with other libraries and tools that may not properly support non-linearities in geometries.

​
Best Practices

To ensure expected behavior when working with geometries, it’s recommended to follow these best practices:
  1. Use language specific geometry libraries for creating, parsing and serializing geometries.
  2. Define polygon exterior rings with a counter-clockwise winding order.
  3. Define polygon holes (interior rings) with a clockwise winding order.
  4. Ensure longitude values are within [-180, 180] and latitude values are within [-90, 90].
  5. For geometries crossing the antimeridian, cut them along the antimeridian into two parts: one for the eastern hemisphere and one for the western.
  6. Define geometries covering a pole in a specific way for correct handling.
  7. When downloading geometries from external sources (for example from STAC Catalogs), always verify these assumptions to prevent unexpected behavior before ingesting them into Tilebox.

​
Geometry vs Geography

Some systems distinguish between Geometry and Geography data types. The primary distinction lies in how edge interpolation is handled along the antimeridian. Geometry represents a shape in an arbitrary 2D Cartesian coordinate system and does not perform edge interpolation. In contrast, Geography typically wraps around the antimeridian by performing edge interpolation, such as converting Cartesian coordinates to a 3D spherical coordinate system. Typically, Geography types limit x coordinates to [-180, 180] and y coordinates to [-90, 90], whereas Geometry types have no such limitations. Tilebox does not differentiate between Geometry and Geography types. Instead, it offers a query option to specify a coordinate reference system. This controls whether geometry intersections and containment checks are performed in a 3D spherical coordinate system (which correctly handles antimeridian crossings) or a standard 2D Cartesian lat/lon coordinate system.

​
Terminology

Familiarize yourself with key geometry concepts.
A great resource to learn more about these concepts is this blog post by Tom MacWright.
Point A Point is a specific location on the Earth’s surface, represented by a longitude and latitude coordinate. Ring A Ring is a collection of points that form a closed loop. The order of the points within the ring matter, since that defines the winding order of the ring, which is either clockwise or counter-clockwise. Every ring should be explicitly closed, meaning that the first and last point should be the same. Polygon A Polygon is a collection of rings. The first ring, the exterior ring defines the polygon’s boundary. Any other rings are called interior rings, representing holes within the polygon. MultiPolygon A MultiPolygon is a collection of polygons.

​
Geometry libraries and common formats

Geometries can be expressed in different formats. The Tilebox Client SDKs delegate geometry handling to external, well-known libraries.
Client SDKGeometry library used by Tilebox
PythonShapely
GoOrb
Here is an example of how to define a Polygon geometry, covering the area of the state of Colorado using Tilebox Client SDKs. 
from shapely import Polygon

area = Polygon(
    ((-109.05, 41.00), (-109.045, 37.0), (-102.05, 37.0), (-102.05, 41.00), (-109.05, 41.00)),
)
These libraries also enable Tilebox to support common geometry formats.

​
GeoJSON

GeoJSON is a geospatial data interchange format based on JavaScript Object Notation (JSON).
colorado.geojson
{
    "type": "Polygon",
    "coordinates": [
        [
            [-109.05, 41.0],
            [-109.045, 37.0],
            [-102.05, 37.0],
            [-102.05, 41.0],
            [-109.05, 41.0]
        ]
    ]
}
Reading such a GeoJSON geometry can be achieved as follows. 
from shapely import from_geojson

with open("colorado.geojson", "r") as f:
    area = from_geojson(f.read())

​
Well-Known Text (WKT)

Well-Known Text (WKT) is a text markup language for representing vector geometry objects. 
from shapely import from_wkt

wkt = "POLYGON ((-109.05 41, -109.045 37, -102.05 37, -102.05 41, -109.05 41))"
area = from_wkt(wkt)

​
Well-Known Binary (WKB)

Well-Known Binary (WKB) is a binary representation of vector geometry objects, a binary equivalent to WKT. Given a colorado.wkb file containing a binary encoding of the Colorado polygon, it can be read as follows. 
from shapely import from_wkb

with open("colorado.wkb", "rb") as f:
    area = from_wkb(f.read())
There is also an extended well known binary format (ewkb) that supports additional information such as specifying a spatial reference system (like EPSG:4326) in the encoded geometry. Pythons shapely library supports this out of the box, and the orb library for Go supports it as well via the github.com/paulmach/orb/encoding/ewkb package.

​
Winding Order

A ring’s winding order defines its orientation (clockwise or counter-clockwise), determined by the sequence of its points. Geometries in Tilebox follow the right hand rule defined by the GeoJSON specification:
A linear ring MUST follow the right-hand rule with respect to the area it bounds, i.e., exterior rings are counterclockwise, and holes are clockwise.
Thus, polygon exterior rings must have a counter-clockwise winding order, and interior rings must have a clockwise winding order. Failing to follow this rule can lead to unexpected query results, as shown below. Take the following Polygon consisting of the same exterior ring but in different winding orders.
Counter-clockwise
POLYGON (
  (-5 56, -6 29, 14 28, 23 55, -5 56)
)
Clockwise
POLYGON (
  (-5 56, 23 55, 14 28, -6 29, -5 56)
)
This is how those two geometries would be interpreted on a sphere.
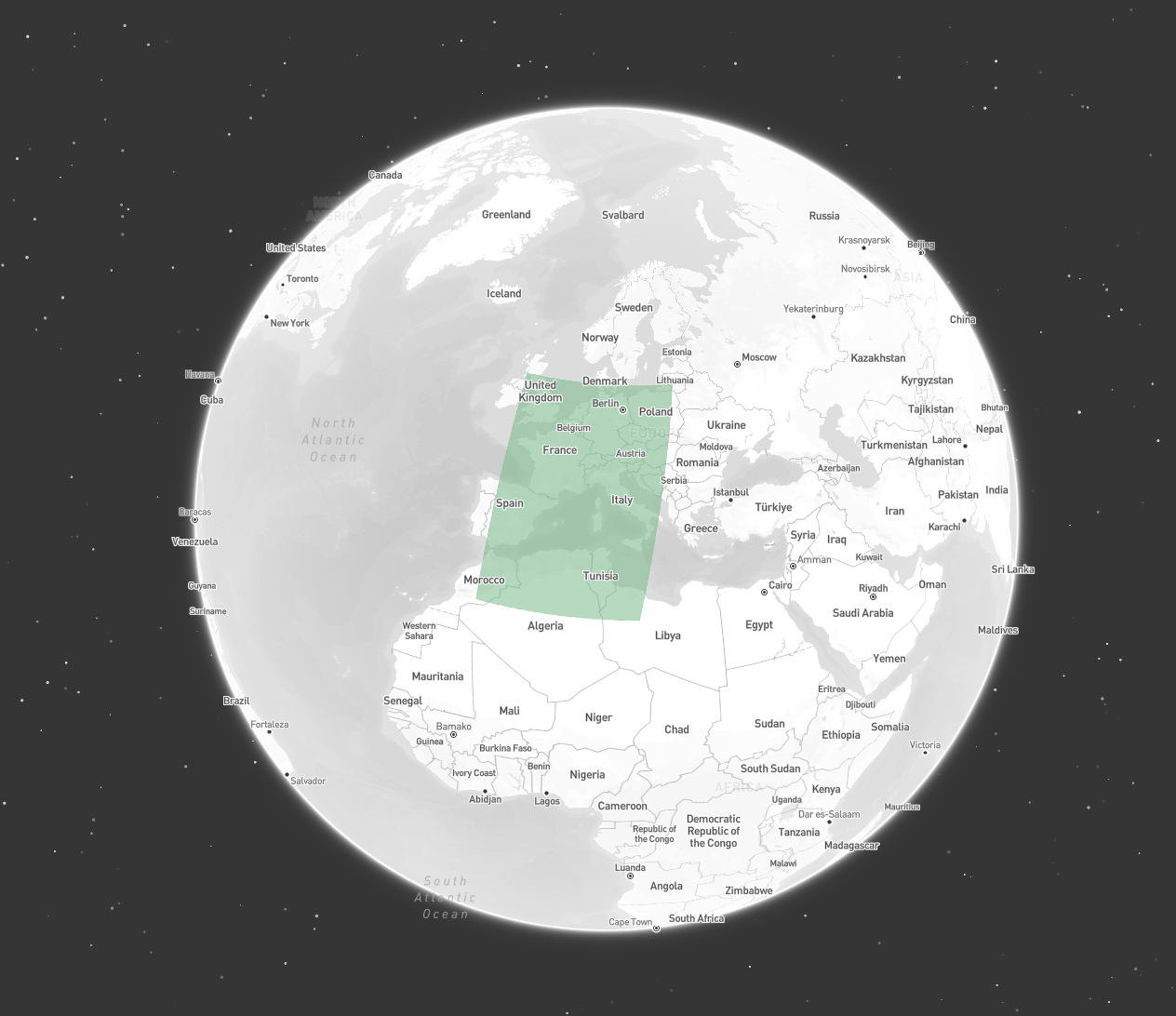
Polygon over Europe with correct winding order

Correct (counter-clockwise) winding order

Polygon covering the whole globe with a hole over Europe due to incorrect winding order

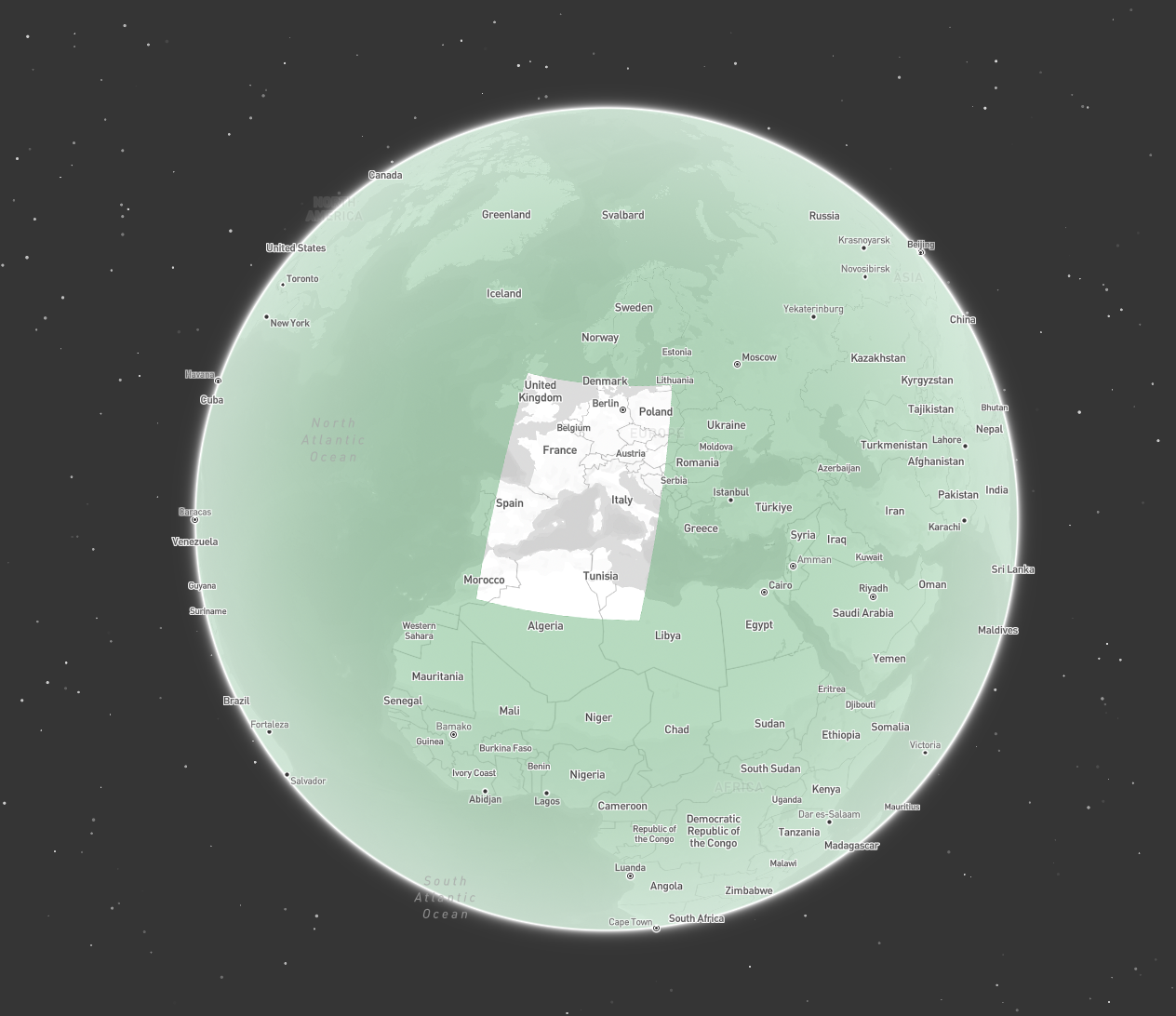
Incorrect (clockwise) winding order

Tilebox automatically detects and corrects incorrect winding orders during data ingestion.
Since such unexpected behavior can cause issues and be hard to debug, Tilebox detects incorrect winding orders and automatically fixes them during ingestion. This means that geometries covering nearly the entire globe except for a small holes cannot be ingested into Tilebox by simply specifying them as a Polygon with an exterior ring in clockwise winding order. Instead, such geometries should be defined as a Polygon consisting of two rings:
  • an exterior ring covering the whole globe in counter-clockwise winding order
  • an interior ring specifying the hole in clockwise winding order
Such a definition, as shown below, ensures correct interpretation by Tilebox, and is also valid according to the GeoJSON specification.
Polygon covering the whole globe with a hole over Europe
POLYGON (
  (-180 90, -180 -90, 180 -90, 180 90, -180 90),
  (-5 56, 23 55, 14 28, -6 29, -5 56)
)
To verify the winding order of a geometry, you can use the following code snippets. 
from shapely import Polygon

polygon = Polygon(
    ((-109.05, 41.00), (-109.045, 37.0), (-102.05, 37.0), (-102.05, 41.00), (-109.05, 41.00)),
)
print(polygon.exterior.is_ccw)  # True

​
Antimeridian Crossings

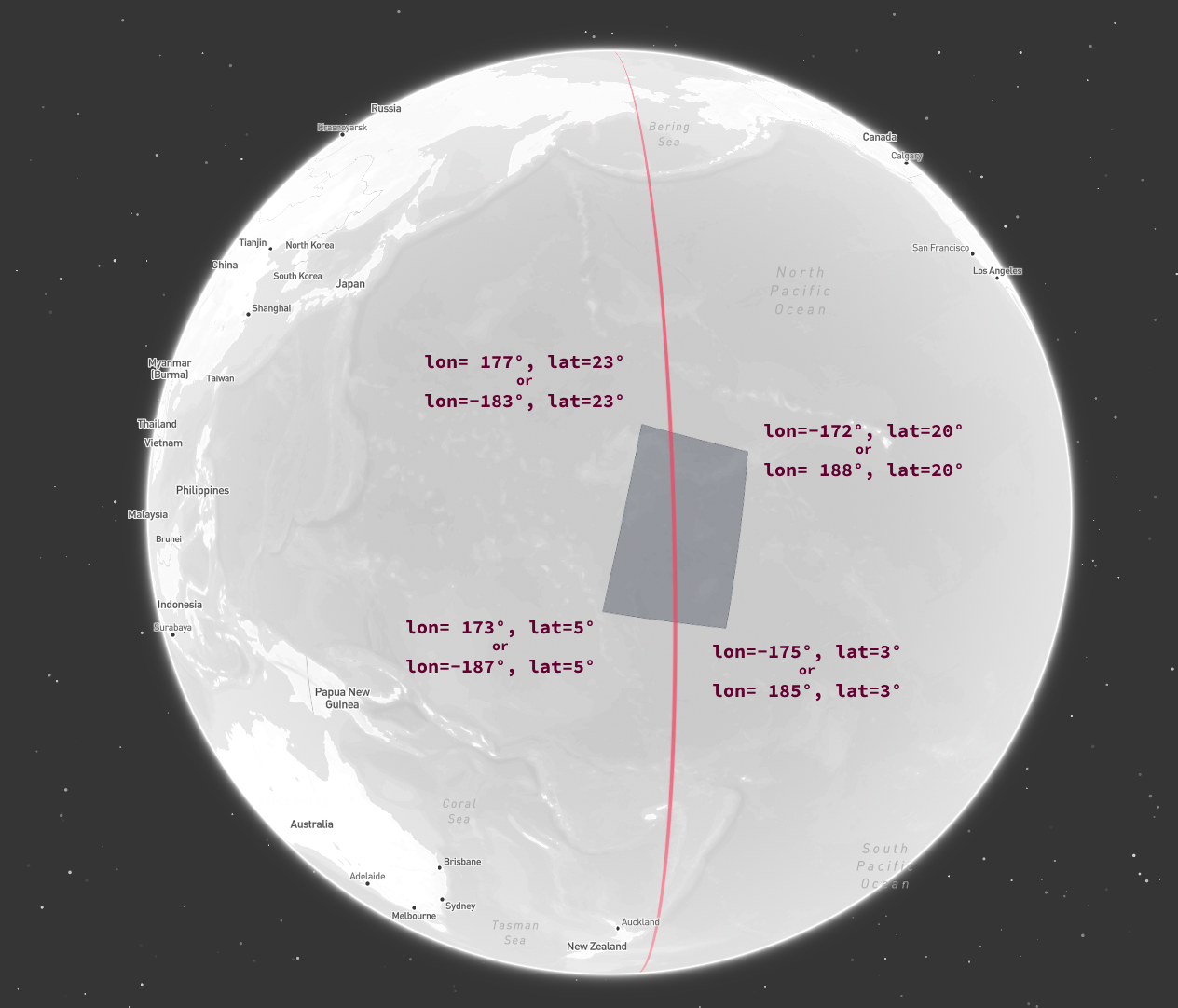
Geometries that cross the antimeridian are a common in satellite data, but can cause issues when not handled correctly. Take the following Polygon that crosses the antimeridian.
Polygon crossing the antimeridian

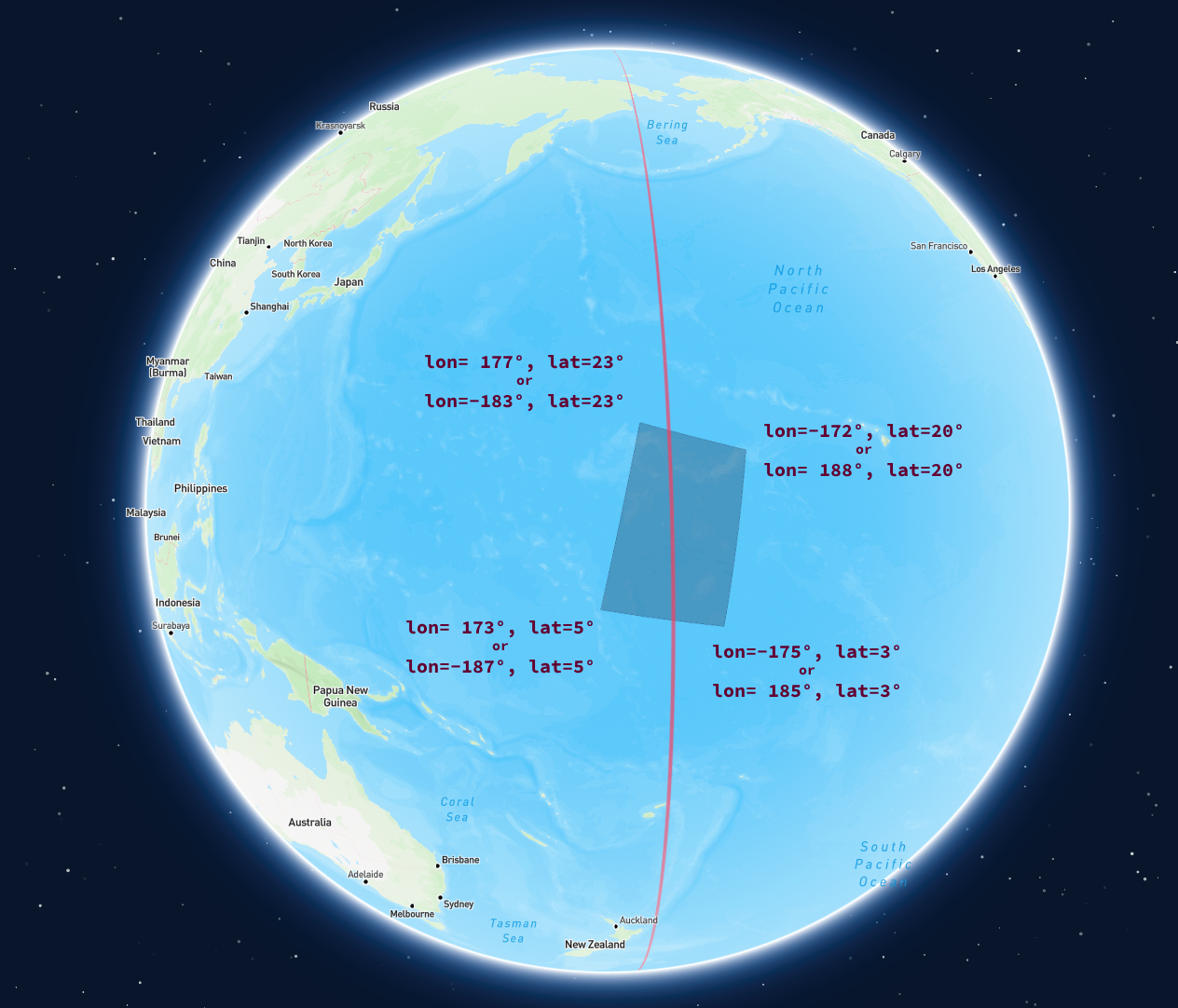
A geometry that crosses the antimeridian

Below are a couple of different ways to express such a geometry.
Using exact longitude / latitude coordinates for each point
POLYGON ((173 5, -175 3, -172 20, 177 23, 173 5))
While valid, this representation can cause issues for many libraries performing calculations or visualizations in a Cartesian coordinate system. The line segment from lon=173 to lon=-175 is interpreted as a 348-degree line crossing the null meridian, spanning nearly the entire globe. Visualizations of such geometries often appear as shown below.
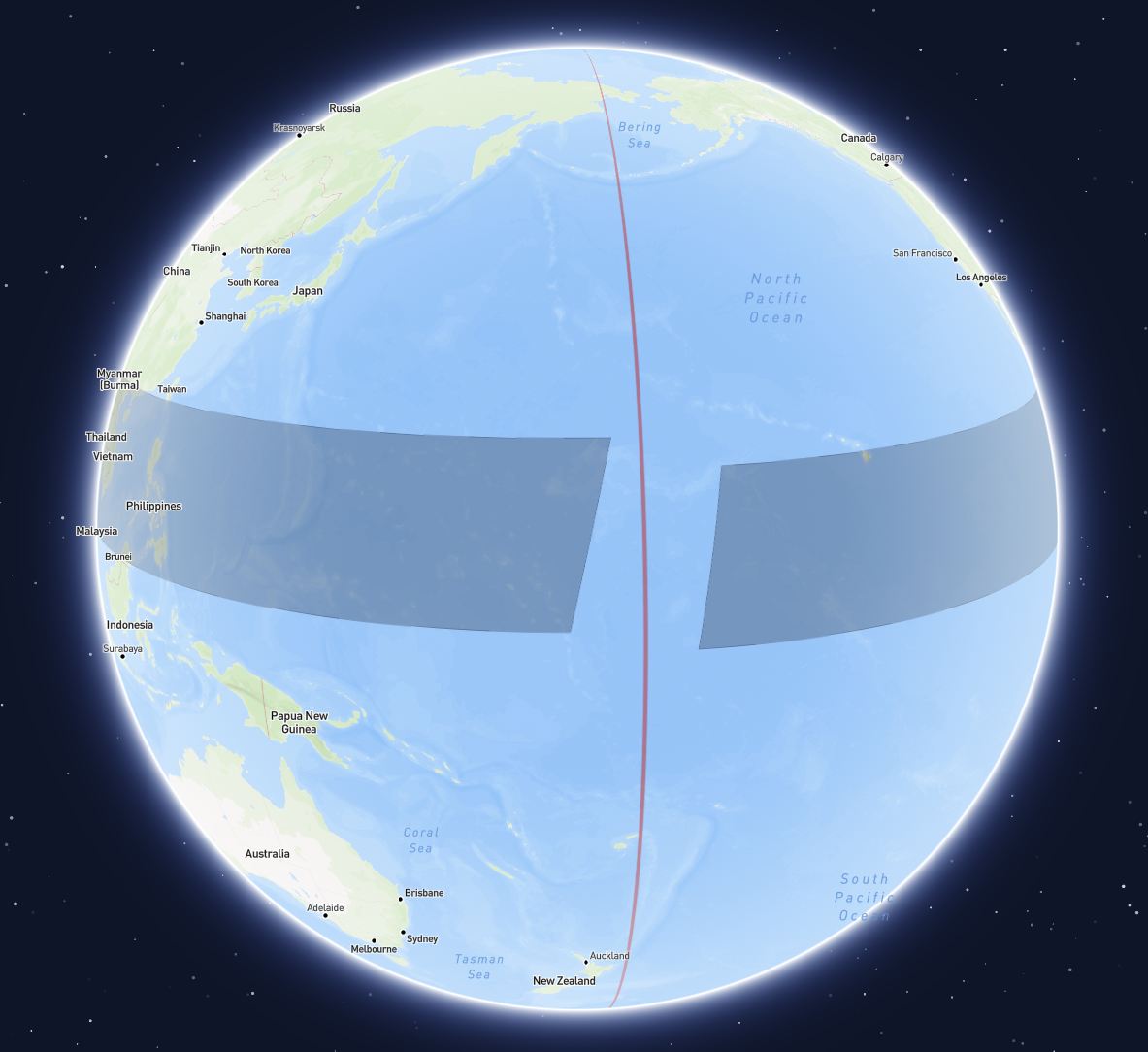
Polygon crossing the antimeridian

Incorrect handling of a geometry crossing the antimeridian

To mitigate these issues, some Cartesian coordinate tools extend the longitude range beyond the usual [-180, 180] bounds. Expressing the geometry in such a way, may look like this.
Extending the longitude range beyond 180
POLYGON ((173 5, 185 3, 188 20, 177 23, 173 5))
Or, the exact same area on the globe can also be expressed as a geometry by extending the longitude range below -180.
Extending the longitude range below -180
POLYGON ((-187 5, -175 3, -172 20, -183 23, -187 5))
While most visualization tools may handle such geometries correctly, special care is required for intersection and containment checks. The following code snippet demonstrates this by constructing a Polygon that covers the same area using both methods and checking for intersection (which should logically occur, as they represent the same geographic area).
Incorrect intersection check
from shapely import from_wkt

a = from_wkt("POLYGON ((173 5, 185 3, 188 20, 177 23, 173 5))")
b = from_wkt("POLYGON ((-187 5, -175 3, -172 20, -183 23, -187 5))")

print(a.intersects(b))  # False

​
Antimeridian Cutting

Additionally, none of the representations shown are valid according to the GeoJSON specification. The GeoJSON specification does offers a solution for this problem, though, which is Antimeridian Cutting. It suggests always cutting lines and polygons that cross the antimeridian into two parts—one for the eastern hemisphere and one for the western hemisphere. To achieve this, check out the antimeridian python package, and an implementation of it in Go.
The antimeridian python package also is a great resource for learning more about possible antimeridian issues, how the cutting algorithm works and edge cases to be aware of.
Cutting the polygon along the antimeridian
MULTIPOLYGON (
    ((180 22.265994, 177 23, 173 5, 180 3.855573, 180 22.265994)),
    ((-180 3.855573, -175 3, -172 20, -180 22.265994, -180 3.855573))
)
By cutting geometries along the antimeridian:
  • they conform to the GeoJSON specification
  • there is no ambiguity about how to correctly interpret the geometry
  • they are correctly handled by most visualization tools
  • intersection and containment checks yield correct results no matter the coordinate reference system used
  • all longitude values are within the valid [-180, 180] range, making it easier to work with them

​
Pole Coverings

Geometries covering a pole can be particularly challenging to handle correctly. No single algorithm addresses all cases, and different libraries and tools may interpret them differently. Often, providing prior knowledge, such as confirming that a geometry is intended to cover a pole, can resolve these issues. For an example of this, check out the relevant section in the antimeridian documentation. Generally speaking though, there are two approaches that work well:

​
Approach 1: Cutting out a hole

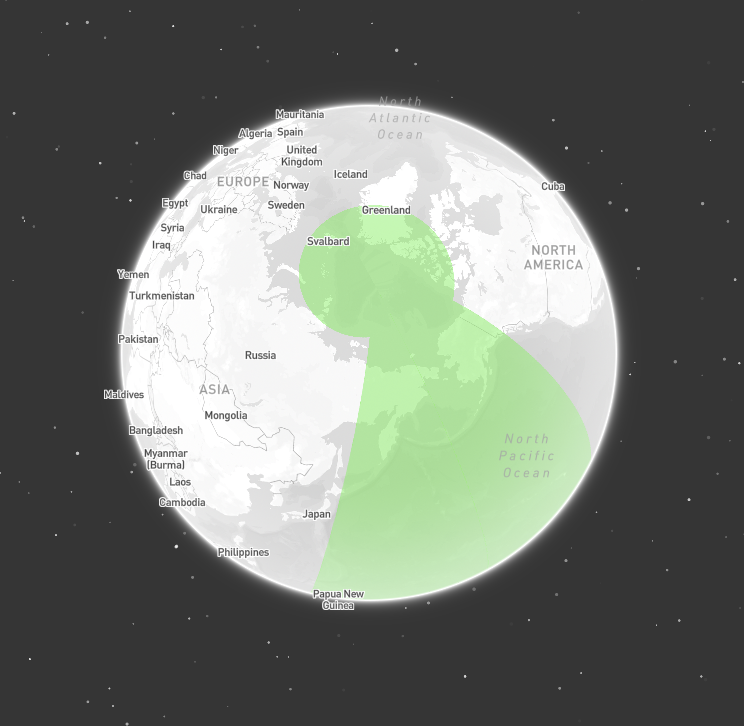
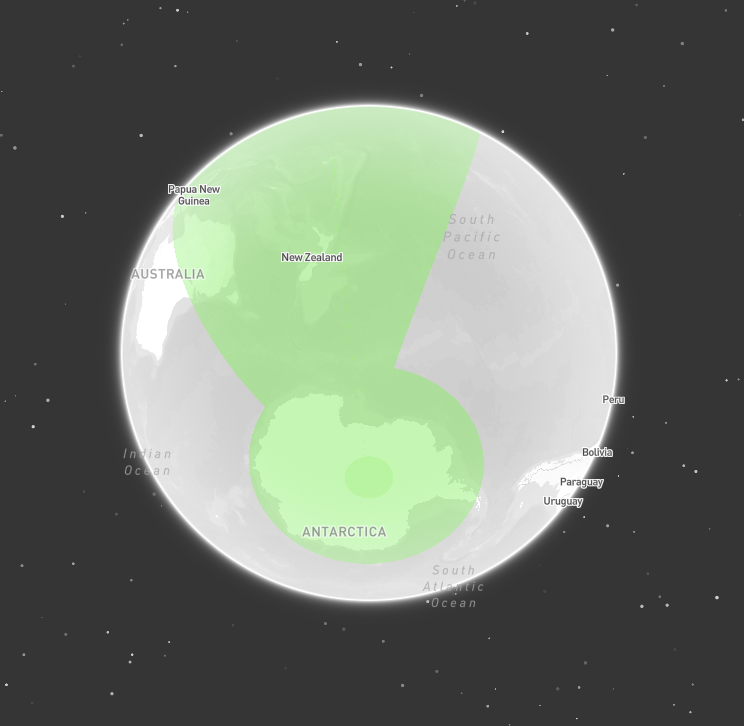
Define a geometry with an exterior ring that covers the whole globe. Then, cut out a hole by defining an interior ring of the area that not covered by the geometry.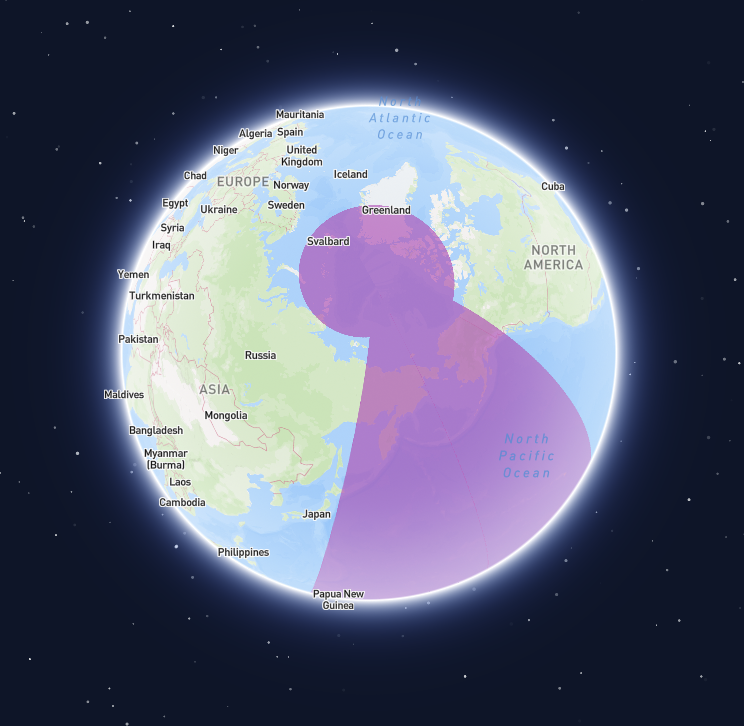
This approach works especially well for geometries that cover both poles, since then the interior ring is guaranteed to not cover any poles.
Polygon covering both poles, viewing north pole covering

Geometry covering both poles (view of north pole)

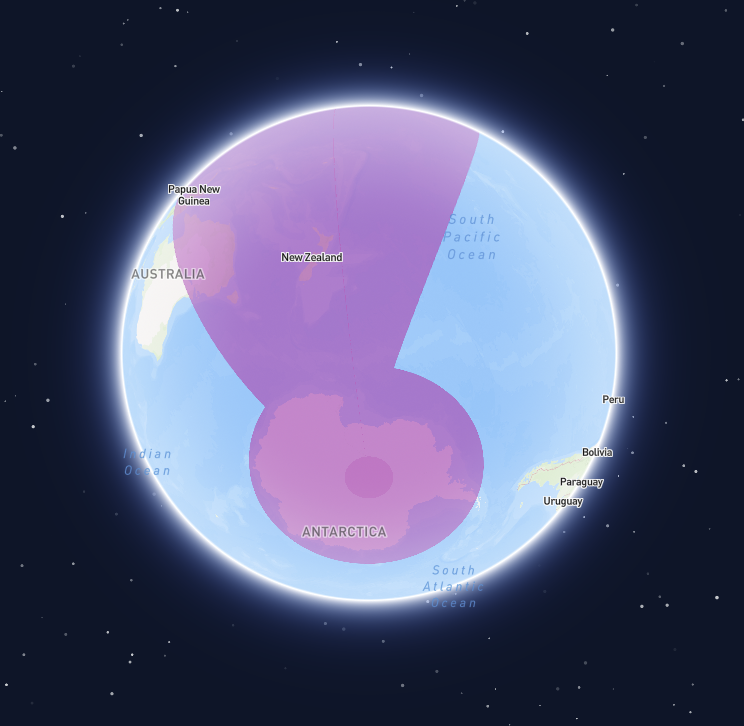
Polygon covering both poles, viewing south pole covering

Geometry covering both poles (view of south pole)

Polygon covering both poles
POLYGON (
    (-180 90, -180 -90, 180 -90, 180 90, -180 90), 
    (-133 72, 153 77, 130 -64, -160 -66, -133 72)
)

​
Approach 2: Splitting into multiple parts

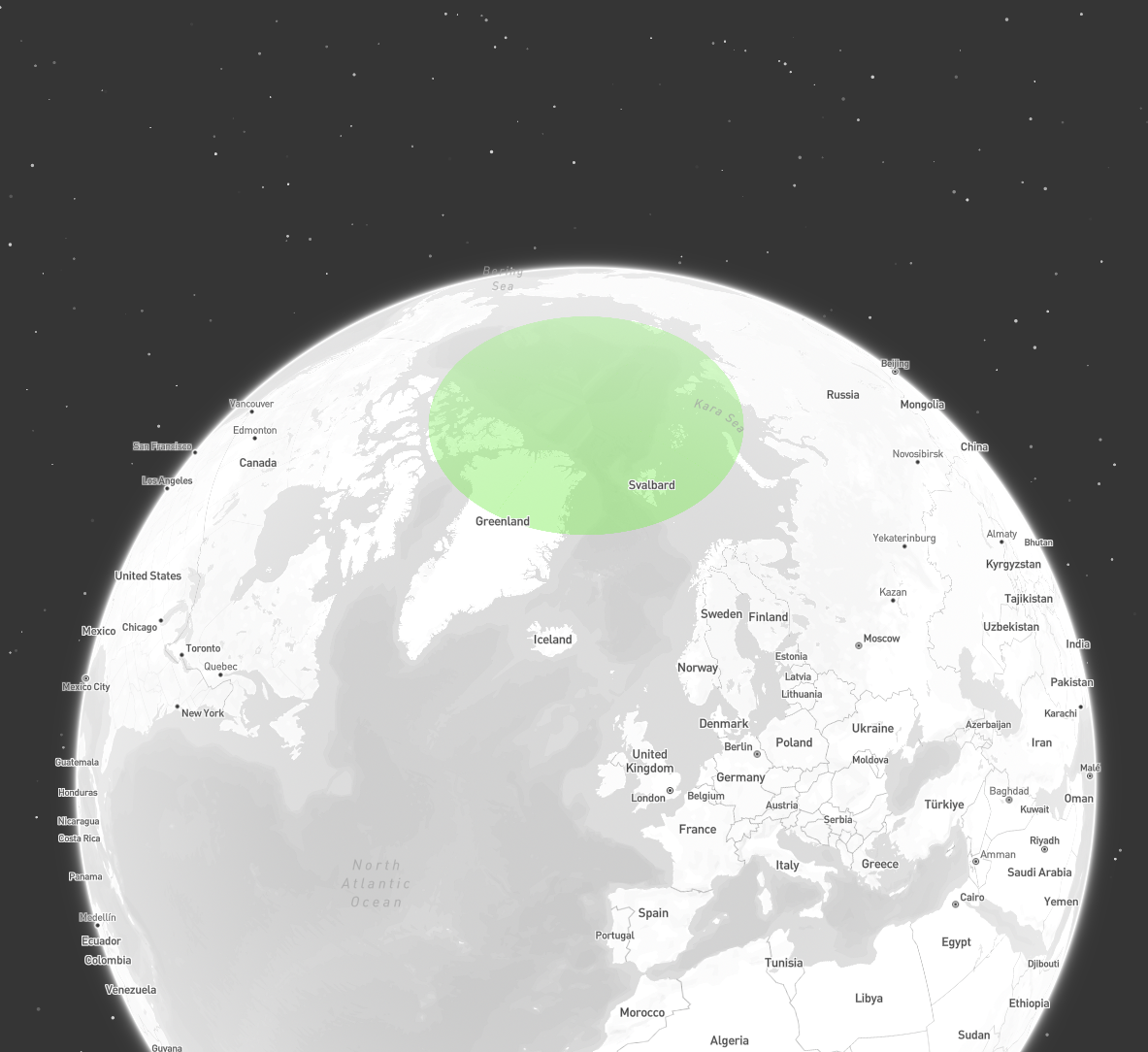
Another approach, effective for circular caps covering a pole, involves cutting the geometry into multiple parts. Instead of splitting the geometry only at the antimeridian, also split it at the null meridian, and the 90 and -90 meridians. For a circular cap covering the north pole, this results in four triangular parts, which can be combined into a MultiPolygon. Visualization libraries and intersection/containment checks performed in cartesian coordinate space will typically handle such a geometry correctly.
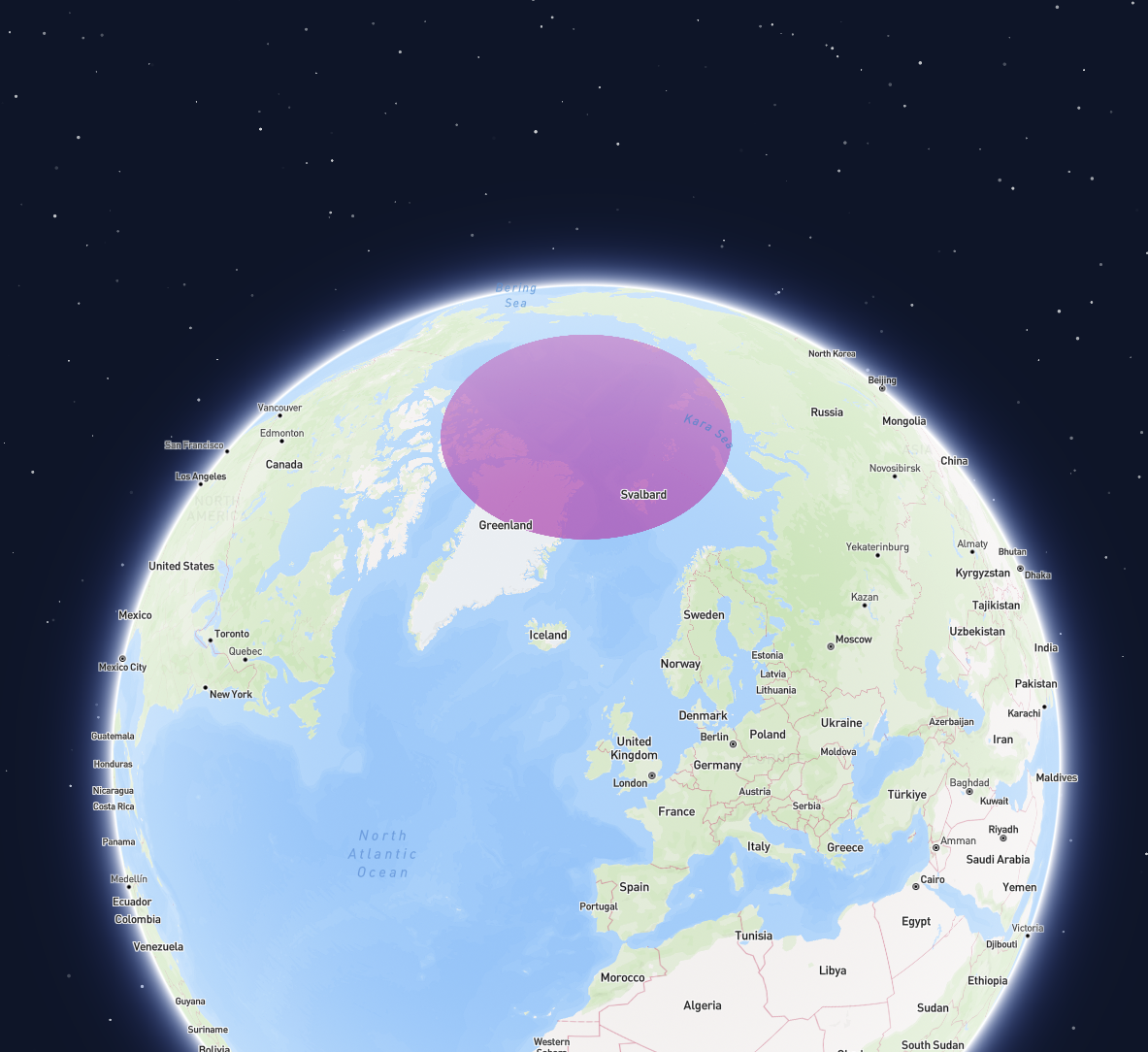
Polygon covering a pole

A geometry covering the north pole

Geometry of a circular cap covering the north pole
MULTIPOLYGON (
    ((-90 75, 0 75, 0 90, -90 90, -90 75)),
    ((0 75, 90 75, 90 90, 0 90, 0 75)),
    ((90 75, 180 75, 180 90, 90 90, 90 75)),
    ((-180 75, -90 75, -90 90, -180 90, -180 75))
)